CANADA'S WINDVIEW

趣味の写真を投稿していきます。昆虫好きな長男と一緒に昆虫を追いかけています。最初の年はセミやカマキリ、次の年はカブトムシ、トンボ、そして今年は…

数列 - 2項間漸化式(特性方程式)

数学・幾何学

カテゴリー[ 昆虫| 田園| 花| 街| 数学・幾何学| 寺院| 城| 祭り| 鉄道| 海| 風力発電]

数列 - 2項間漸化式(特性方程式)

2項間漸化式の一般項

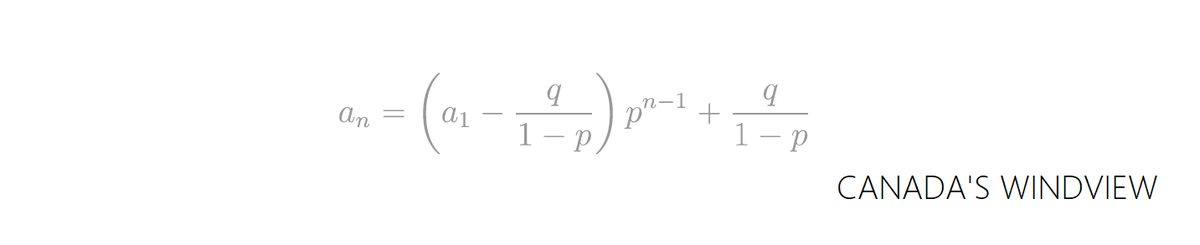
数列の2項間漸化式の解法で、特性方程式を用いるタイプです。

a_{n + 1} = p a_{n} + q \ \ \ ( p \neq 0, 1 ) \tag{1}

という関係を持つ数列 \{ a_{n} \} の一般項を求めます。

a_{n + 1} - \alpha = p ( a_{n} - \alpha )  \tag{2}

という等比数列の形にしたいので、 (2) を変形して、

(2) \Leftrightarrow a_{n + 1} = p a_{n} - p \alpha + \alpha \tag{3}

(1) と比較して、

q = - p \alpha + \alpha = \alpha ( 1 - p )

\displaystyle \Leftrightarrow \alpha = \frac{ q }{ 1 - p } \tag{4}

拠って元の式 (1) は、

\displaystyle a_{n + 1} - \frac{ q }{ 1 - p } = p \left( a_{n} - \frac{ q }{ 1 - p } \right) \tag{5}

と表せます。

ここで、新たに数列 \{ b_{n} \} を

\displaystyle b_{n} = a_{n} - \frac{ q }{ 1 - p } \tag{5}

と置くと、

\displaystyle b_{1} = a_{1} - \frac{ q }{ 1 - p } \tag{6}

であり、 (5) 式は、

  b_{n + 1} = p b_{n} \tag{7}

という等比数列と捉えることが出来ます。これより数列 \displaystyle \{ b_{n} \} の一般項は、

  b_{n} = b_{1} p^{n - 1} \tag{8}

となります。これと (5)， (6) より、

\displaystyle a_{n} - \frac{ q }{ 1 - p } = \left( a_{1} - \frac{ q }{ 1 - p } \right) p^{n - 1}

\displaystyle \Leftrightarrow a_{n} = \left( a_{1} - \frac{ q }{ 1 - p } \right) p^{n - 1} + \frac{ q }{ 1 - p } \tag{9}