カテゴリー[ 昆虫| 田園| 花| 街| 数学・幾何学| 寺院| 城| 祭り| 鉄道| 海| 風力発電]
累乗の和 - 八乗和の公式
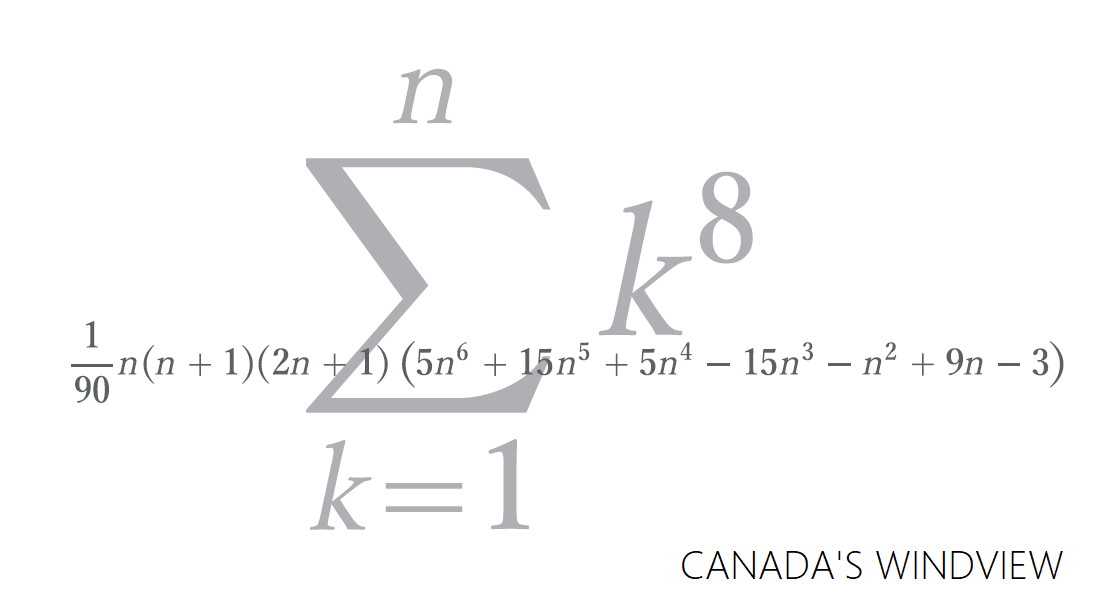
八乗和の公式の導出です。
更に(1)と、七乗和、六乗和、五乗和、四乗和、三乗和、二乗和の公式から、
<関連>
九乗和の公式
七乗和の公式
六乗和の公式
五乗和の公式(3)
五乗和の公式(2)
五乗和の公式
四乗和の公式(2)
四乗和の公式
三乗和の公式(3)
三乗和の公式(2)
三乗和の公式
二乗和の公式(2)
二乗和の公式
等比数列の和の公式
パスカルの三角形
式の展開、因数分解
九乗和の公式
七乗和の公式
六乗和の公式
五乗和の公式(3)
五乗和の公式(2)
五乗和の公式
四乗和の公式(2)
四乗和の公式
三乗和の公式(3)
三乗和の公式(2)
三乗和の公式
二乗和の公式(2)
二乗和の公式
等比数列の和の公式
パスカルの三角形
式の展開、因数分解