楕円の方程式

カテゴリー[ 昆虫| 田園| 花| 街| 数学・幾何学| 寺院| 城| 祭り| 鉄道| 海| 風力発電]

楕円の定義

2つの定点(焦点)からの距離の和が一定の点の集合です。

楕円の方程式

i) $a$ ＞ $b$ ＞ $0$ の時

$a$ ＞ $b$ ＞ $0$ の時、楕円の方程式は、

$\large \displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

と表せます。長軸の長さは $2 a$ 、短軸の長さは $2 b$ となります。

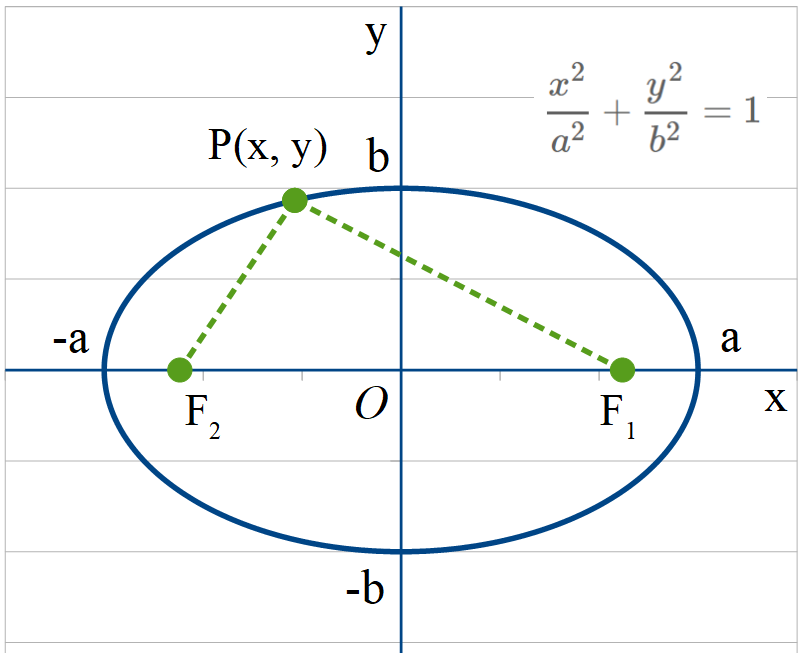
f:id:windview_canada:20211201220105p:plain — 楕円の方程式のグラフ01

この時、2焦点 $F_1$ ， $F_2$ の座標はそれぞれ、

$F_1 \left( \sqrt{ a^2 - b^2 } , 0 \right)$ ， $F_2 \left( - \sqrt{ a^2 - b^2 } , 0 \right)$

となります。図のような直角三角形を考えれば、容易に導出できます。

f:id:windview_canada:20211201220229p:plain — 楕円の方程式の焦点の座標の求め方01

ii) $b$ ＞ $a$ ＞ $0$ の時

$b$ ＞ $a$ ＞ $0$ の時、楕円の方程式は、i) の場合と同じですが、長軸の長さは $2 b$ 、短軸の長さは $2 a$ と変わります。

2焦点 $F_1$ ， $F_2$ の座標はそれぞれ、

$F_1 \left( 0, \sqrt{ b^2 - a^2 } \right)$ ， $F_2 \left( 0, - \sqrt{ b^2 - a^2 } \right)$

と変わります。

導出

楕円の方程式を導出します。

$a$ ＞ $b$ ＞ $0$ の時、

楕円上の点 $P ( x , y )$ について、

$F_1 P + F_2 P = 2 a$ (一定)

より、

$\sqrt{ \left( \sqrt{ a^2 - b^2 } - x \right)^2 + y^2 } + \sqrt{ \left( \sqrt{ a^2 - b^2 } + x \right)^2 + y^2 } = 2 a \\ \Leftrightarrow \sqrt{ \left( \sqrt{ a^2 - b^2 } - x \right)^2 + y^2 } = 2 a - \sqrt{ \left( \sqrt{ a^2 - b^2 } + x \right)^2 + y^2 }$

両辺2乗して、

$\left( \sqrt{ a^2 - b^2 } - x \right)^2 + y^2 = 4 a^2 - 4 a \sqrt{ \left( \sqrt{ a^2 - b^2 } + x \right)^2 + y^2 } + \left( \sqrt{ a^2 - b^2 } + x \right)^2 + y^2 \\ \Leftrightarrow \left( \sqrt{ a^2 - b^2 } - x \right)^2 = 4 a^2 - 4 a \sqrt{ \left( \sqrt{ a^2 - b^2 } + x \right)^2 + y^2 } + \left( \sqrt{ a^2 - b^2 } + x \right)^2 \\ \Leftrightarrow \left( a^2 - b^2 \right) - 2 x \sqrt{ a^2 - b^2 } + x^2 = 4 a^2 - 4 a \sqrt{ \left( \sqrt{ a^2 - b^2 } + x \right)^2 + y^2 } + \left( a^2 - b^2 \right) + 2 x \sqrt{ a^2 - b^2 } + x^2 \\ \Leftrightarrow - 2 x \sqrt{ a^2 - b^2 } = 4 a^2 - 4 a \sqrt{ \left( \sqrt{ a^2 - b^2 } + x \right)^2 + y^2 } + 2 x \sqrt{ a^2 - b^2 } \\ \Leftrightarrow 4 a \sqrt{ \left( \sqrt{ a^2 - b^2 } + x \right)^2 + y^2 } = 4 a^2 + 4 x \sqrt{ a^2 - b^2 } \\ \Leftrightarrow a \sqrt{ \left( \sqrt{ a^2 - b^2 } + x \right)^2 + y^2 } = a^2 + x \sqrt{ a^2 - b^2 }$

更に両辺を2乗して、

$a^2 \left\{ \left( \sqrt{ a^2 - b^2 } + x \right)^2 + y^2 \right\} = a^4 + 2 a^2 x \sqrt{ a^2 - b^2 } + x^2 \left( a^2 - b^2 \right) \\ \Leftrightarrow a^2 \left( a^2 - b^2 + 2 x \sqrt{ a^2 - b^2 } + x^2 + y^2 \right) = a^4 + 2 a^2 x \sqrt{ a^2 - b^2 } + a^2 x^2 - b^2 x^2 \\ \Leftrightarrow a^4 -a^2 b^2 + 2 a^2 x \sqrt{ a^2 - b^2 } + a^2 x^2 + a^2 y^2 = a^4 + 2 a^2 x \sqrt{ a^2 - b^2 } + a^2 x^2 - b^2 x^2 \\ \Leftrightarrow b^2 x^2 + a^2 y^2 = a^2 b^2 \Leftrightarrow \displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$