カテゴリー[ 昆虫| 田園| 花| 街| 数学・幾何学| 寺院| 城| 祭り| 鉄道| 海| 風力発電]
正五角形と黄金比(2)
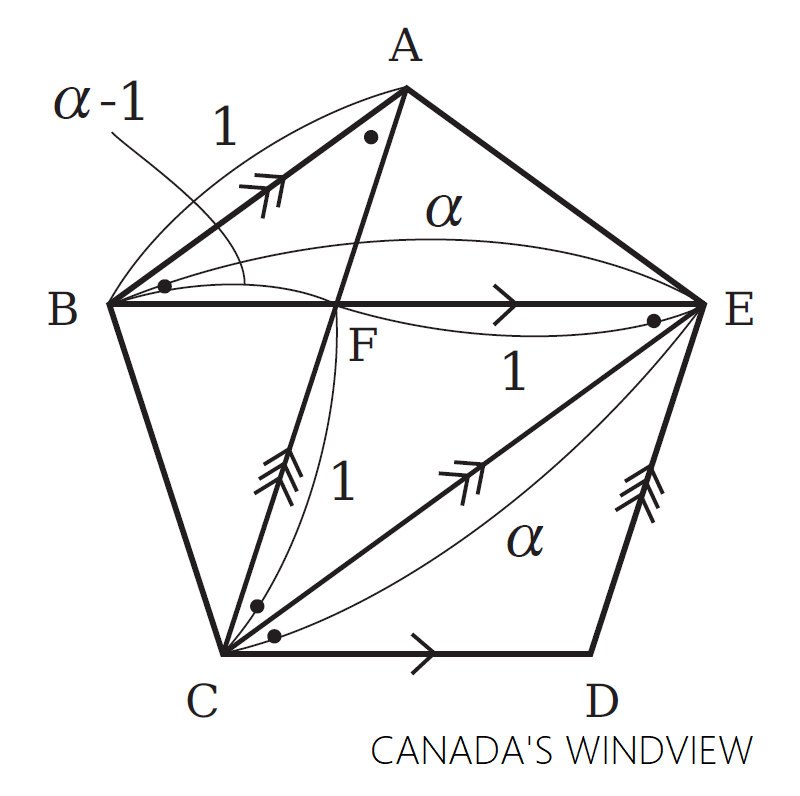
一辺の長さが の正五角形
の対角線
の長さ
を求めるもう一つのアプローチです。
先ず、 と
の交点を
とします。
そうすると、,
と
より、
は菱形であることが判ります。
これより、 なので
は二等辺三角形となり、
も
で二等辺三角形と言えます。更に
より
,
の為、
と言えます。
これより、次の関係式が成り立ちます。
これから を求めるのですが、求め方は「正五角形と黄金比」のページで詳しく解説しています。